■解答
(イ) \(B_0\left(1-\displaystyle\frac{r}{R}\right)\) (ロ) \(er\omega B_0 \left(1-\displaystyle\frac{r}{R}\right)\) (ハ) \(r\omega B_0\left(1-\displaystyle\frac{r}{R}\right)\) (ニ) \(\displaystyle\frac{1}{6}\omega B_0 R^2\) (ホ) \(\left(1-\displaystyle\frac{r}{R}\right)B_0 \Delta S\)
問1 \(\pi a^2 B_0 \left(1-\displaystyle\frac{2a}{3R}\right)\)
(へ) \(\displaystyle\frac{ab}{2}\left(1-\frac{2a}{3R}\right)\) (ト) \(\displaystyle\frac{abe}{2m}\left(1-\frac{2a}{3R}\right)t\)
問2 \(\displaystyle\frac{3}{4}\)
■解説
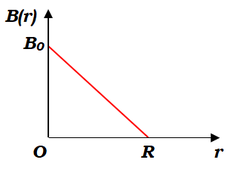
(イ) 図1を活用して\(B-r\)グラフを描くと、このようになる。
これによって、
\(B(r)=-\displaystyle\frac{B_0}{R}r+B_0\)
\(=B_0\displaystyle\left(1-\frac{r}{R}\right)\)
(ロ) ローレンツ力の公式より、ローレンツ力の大きさは、
\(|F|=evB\)
ここに、\(v=r\omega\)と\(B=B_0\displaystyle\left(1-\frac{r}{R}\right)\)を代入すると、
\(|F|=er\omega B_0\left(1-\displaystyle\frac{r}{R}\right)\)
(ハ) 電場による力と、ローレンツ力とがつり合っているので、
\(eE=er\omega B_0\left(1-\displaystyle\frac{r}{R}\right)\)
\(E=r\omega B_0\left(1-\displaystyle\frac{r}{R}\right)\)
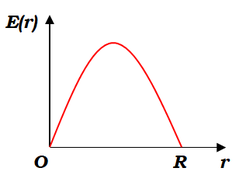
(ニ) \(E=\omega B_0r\left(1-\frac{r}{R}\right)\)
\(=\displaystyle\frac{\omega B_0}{R}・r(R-r)\)
となるので、\(E-r\)グラフを描くと、図のように上に凸の二次関数となる。
ここで、頂点の座標は解くのに重要となる値ではないので、特に計算せずにグラフの概形だけを表している。
この面積が導体棒の両端間の電位差になるので、
面積\(=\displaystyle\frac{\omega B_0}{R}・\frac{1}{6}R^3\)
\(=\displaystyle\frac{1}{6}\omega B_0 R^2\)
(ホ) \(\Delta S\)は微小なので、\(\Delta S\)内の\(B(r)\)は一定であるとみなせる。
\(\Delta \Phi=B(r)・\Delta S\)
\(=\left(1-\displaystyle\frac{r}{R} \right) B_0 \Delta S\)

問1
問題文に「\(\Phi_R\)は円内の\(\Delta \Phi\)の総和であり、\(\Phi_R=\displaystyle\frac{1}{3}\pi R^2 B_0\)となる」とあるが、これは\(B(r)\)を高さとみなしたときの立体の体積として求めることができることを意味している。
よって
\(\phi_a=\pi a^2B_0\left(1-\displaystyle\frac{a}{R}\right) +\displaystyle\frac{1}{3}\pi a^2・\frac{a}{R}B_0\)
\(=\pi a^2 B_0-\displaystyle\frac{\pi a^3 B_0}{R}+\frac{\pi a^3 B_0}{3R}\)
\(=\pi a^2 B_0-\displaystyle\frac{2\pi a^3 B_0}{3R}\)
\(=\pi a^2 B_0 \left(1-\displaystyle\frac{2a}{3R}\right)\)
問1別解(微積を用いる方法)
\(\Delta S → ds=r dr d\theta\)として、\(r\)と\(\theta\)について二重積分を行う。
\(\phi_a=\displaystyle \int_0^{2\pi} \int_0^a \left(1-\frac{r}{R} \right) B_0・r dr d\theta\)
から、まずは\(\theta\)だけを変数とみなして、\(\theta\)について積分をする。\(B_0\)は定数なので、積分記号の外に出しておく。
\(\phi=2\pi B_0 \displaystyle \int_0^a \left( r-\frac{r^2}{R}\right) dr\)
次に、\(r\)を変数とみなして、\(r\)について積分をする。
\(\phi=2\pi B_0 \left[ \displaystyle\frac{1}{2}r^2-\frac{1}{3R}r^3 \right]_0^a\)
\(=2\pi B_0 \left( \displaystyle\frac{a^2}{2}-\frac{a^3}{3R}\right)\)
\(=\pi B_0 a^2 \left(1-\displaystyle\frac{2a}{3R}\right)\)
(ヘ) 半径\(a\)の円周上で生じる誘導起電力の大きさは、
\(|V_a|=\displaystyle\frac{\Delta \Phi_a}{\Delta t}\)
\(=\displaystyle\frac{\pi a^2 B_0}{t}\left(1-\frac{2a}{3R}\right)\)
\(B_0=bt\)として
\(=\pi a^2 b \left(1-\displaystyle\frac{2a}{3R}\right)\)
電子は半径\(a\)を一定に保ったまま円運動しているので、\(V\)、\(E\)、\(d\)がいずれも一定となり、\(V_a=Ed\)が使える。
\(d=2\pi a\)と考えて、
\(|E|=\displaystyle\frac{\pi a^2 b}{2\pi a}\left(1-\frac{2a}{3R}\right)\)
\(=\displaystyle\frac{ab}{2}\left(1-\frac{2a}{3R}\right)\)
(ト) 電子の、円軌道に沿った方向の加速度を\(A\)とすると、運動方程式は
\(mA=eE\)
\(mA=\displaystyle\frac{abe}{2}\left(1-\frac{2a}{3R}\right)\)
\(A=\displaystyle\frac{abe}{2m}\left(1-\frac{2a}{3R}\right)\)
よって、\(v_0=0\)であるとき
\(v=v_0+at\)
\(=\displaystyle\frac{abe}{2m}\left(1-\frac{2a}{3R}\right)t\)
※この式は、半径\(a\)を保ったままで電子が加速していったときの速さを表す式であって、遠心力が働いているか働いていないかには言及していない。なので、遠心力が働いていて、かつ半径\(a\)を保ったままであることを確かめるには、別の式も利用しなければならない。
問2
遠心力を考慮しても、半径が\(a\)のままであるためには、遠心力とローレンツ力がつり合わなければならない。
よって
\(m\displaystyle\frac{v^2}{a}=evB\)
において、
\(B=B_0\left(1-\displaystyle\frac{a}{R}\right)\)
かつ
\(B_0=bt\)
であるので、
\(m\displaystyle\frac{v^2}{a}=evb\left(1-\frac{a}{R}\right)t\)
\(v=\displaystyle\frac{abe}{m}\left(1-\frac{a}{R}\right)t\)
となる。この値と(ト)は一致するので、
\(\displaystyle\frac{abe}{2m}\left(1-\frac{2a}{3R}\right)t=\frac{abe}{m}\left(1-\frac{a}{R}\right) t\)
\(\displaystyle\frac{1}{2}\left(1-\frac{2a}{3R}\right)=1-\frac{a}{R}\)
\(\displaystyle\frac{1}{2}-\frac{a}{3R}=1-\frac{a}{R}\)
\(\displaystyle\frac{2a}{3R}=\frac{1}{2}\)
\(\displaystyle\frac{a}{R}=\frac{3}{4}\)
