■解答
問1 \(I_0=\displaystyle\frac{E}{R_2}\) 問2 \(I_0'=\displaystyle\frac{E}{R_1+R_2}\) \(P_0=\displaystyle\frac{R_1}{R_2}\frac{E^2}{R_1+R_2}\)
問3 \(\displaystyle\frac{\Delta I_0}{\Delta t}=\frac{E}{L}\frac{R_2}{R_1+R_2}\) \(\displaystyle\frac{\Delta U_0}{\Delta t}=\frac{E^2}{R_1+R_2}\) 問4 \(I_1=\displaystyle\frac{E}{R_1}\) \(U_1=\displaystyle\frac{LE^2}{2R_1^2}\)
問5 \(\displaystyle\frac{\Delta I}{\Delta t}=-\frac{1}{L}(V_N-E)\) 問6 \(I=I_1-\displaystyle\frac{1}{L}(V_N-E)(t-T_1)\)
問7 \(T_2=T_1+\displaystyle\frac{LI_1}{V_N-E}\)
問8 領域Ⅰ(あ) 領域Ⅱ(い) 領域Ⅲ(い)
問9(a) (う) (b) (い)
■解説
問1 初期状態において、コイルを流れる電流\(I_0\)は、定常電流であるから、コイルを導線と見なして、
\(E-R_2I_0=0\)
\(I_0=\displaystyle\frac{E}{R_2}\)
問2
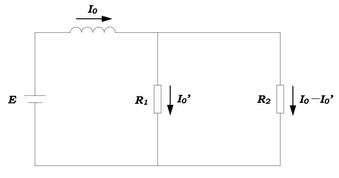
並列部の電位差は等しいので、
\(R_1I_0'=R_2(I_0-I_0')\)
\(=R_2I_0-R_2I_0'\)
\((R_1+R_2)I_0'=R_2I_0\)
\(I_0'=\displaystyle\frac{R_2}{R_1+R_2}I_0\)
消費電力の総量\(P_0\)は、\(R_1\)、\(R_2\)それぞれの消費電力を求めてから和を算出するよりも、合成抵抗を求めて、回路全体を一本化して求める方がラクに解けます。
合成抵抗は、
\(R_{合成}=\displaystyle\frac{積}{和}=\frac{R_1R_2}{R_1+R_2}\) であるから、
消費電力の総量\(P_0\)は、
\(P_0=R_{合成}I_0^2\)
\(=\displaystyle\frac{R_1R_2}{R_1+R_2}・\left( \frac{E}{R_2} \right)^2\)
\(=\displaystyle\frac{R_1R_2}{R_2^2(R_1+R_2)}E^2\)
\(=\displaystyle\frac{R_1}{R_2(R_1+R_2)}E^2\)
問3 回路を合成しておきましょう。
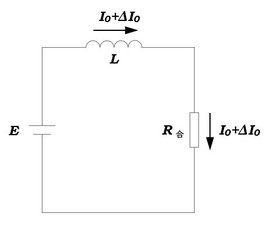
キルヒホッフの第二法則より
\(E-L\displaystyle\frac{\Delta I_0}{\Delta t}=(I_0+\Delta I_0)R_{合成}\)
\(=I_0\left( 1+ \displaystyle\frac{\Delta I_0}{I_0} \right)R_{合成}\)
ここで、\(I_0 \gg \Delta I_0\) より
\(=I_0R_{合成}\)
\(=\displaystyle\frac{E}{R_2}・\frac{R_1R_2}{R_1+R_2}\)
\(=\displaystyle\frac{R_1}{R_1+R_2}E\)
\(L\displaystyle\frac{\Delta I_0}{\Delta t}=E-\displaystyle\frac{R_1}{R_1+R_2}E\)
\(=\displaystyle\frac{R_2}{R_1+R_2}E\)
\(\displaystyle\frac{\Delta I_0}{\Delta t}=\frac{R_2}{R_1+R_2}・\frac{E}{L}\)
また、
\(U_0=\displaystyle\frac{1}{2}LI_0^2\) \(U=\displaystyle\frac{1}{2}L(I_0+\Delta I_0)^2\) より
\(\Delta U= U-U_0'\)
\(=\displaystyle\frac{1}{2}L(I_0^2+2I_0\Delta I_0 +(\Delta I_0)^2)-\frac{1}{2}LI_0^2\)
\(=LI_0\Delta I_0\)
\(\displaystyle\frac{\Delta U}{\Delta t}=LI_0\frac{\Delta I_0}{\Delta t}\)
\(=L・\displaystyle\frac{E}{R_2}・\frac{R_2}{R_1+R_2}・\frac{E}{L}\)
\(\displaystyle\frac{E^2}{R_1+R_2}\)
問5
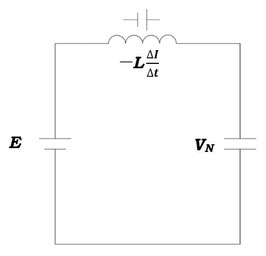
スイッチを切った直後は、電流が流れますが、しばらくしてから発光が停止するということから、\(\Delta I<0\)であることが分かります。
この間のコイルの誘導起電力が、
\(-L\displaystyle\frac{\Delta I}{\Delta t}\) (\(>0\))
になることを考えて、キルヒホッフの法則を使うと、
\(E-L\displaystyle\frac{\Delta I}{\Delta t}=V_N\)
\(L\displaystyle\frac{\Delta I}{\Delta t}=E-V_N\)
\(\displaystyle\frac{\Delta I}{\Delta t}=\frac{1}{L}(E-V_N)\) (\(<0\))、(\(E<V_N\))
問6
\(I=\alpha t+\beta \) において、\(\alpha =\displaystyle\frac{\Delta I}{\Delta t}\)であるから、
\(I=\displaystyle\frac{\Delta I}{\Delta t}t+\beta\)
ここで、\(t=T_1\)のとき、\(I=I_1\)であるから、
\(I_1=\displaystyle\frac{\Delta I}{\Delta t}T_1+\beta\)
\(\beta=I_1-\displaystyle\frac{\Delta I}{\Delta t}T_1\)
よって、
\(I=\displaystyle\frac{\Delta I}{\Delta t}t+I_1-\displaystyle\frac{\Delta I}{\Delta t}T_1\)
\(=\displaystyle\frac{\Delta I}{\Delta t}(t-T_1)+I_1\)
\(=\displaystyle\frac{1}{L}(E-V_N)(t-T_1)+I_1\)
問7
同様に、\(t=T_2\)のとき、\(I=0\)となればいいので、
\(0=\displaystyle\frac{1}{L}(E-V_N)(T_2-T_1)+I_1\)
\(I_1=\displaystyle\frac{1}{L}(V_N-E)(T_2-T_1)\)
\(T_2-T_1=\displaystyle\frac{LI_1}{V_N-E}\)
\(T_2=\displaystyle\frac{LI_1}{V_N-E}+T_1\)
問8
[領域Ⅰ]
\(t=T_0\)で\(I=0\) ⇒ (い)×
コイルはスイッチを入れた直後、最も抵抗値が大きく、その後、直ちに電流が流れ出す ⇒ (う)×
よって(あ)
[領域Ⅱ]
問5より、
\(\displaystyle\frac{\Delta I}{\Delta t}=const.<0\)
よって(い)
[領域Ⅲ]
スイッチオンの瞬間は断線状態と見なせるので、\(V=0\)
その後しばらくすると、コイルは導線と見なすことができるので、\(V=E\)
よって(い)
問9
問6において、\(L\longmapsto 2L\)と置換すると、
\(I'=\displaystyle\frac{1}{2L}(E-V_N)(t-T_1)+I_1\)
ここで\(t=T_1\)のとき、
\(I'=I_1\)
よって、光りはじめは、\(\underset{(a)(う)}{\underline{同じ}}\)明るさとなる。
また、ネオン管の発光停止時間を\(t=T_2\)とすると、問7より、
\(T_2-T_1=\displaystyle\frac{LI_1}{V_N-E}\)
と書けるが、\(L\longmapsto 2L\)と置換すると、
\(2(T_2-T_1)=\displaystyle\frac{2LI_1}{V_N-E}\)
となり、発光時間も、\(\underset{(b)(い)}{\underline{2倍}}\)となる。
