コンデンサーの充電
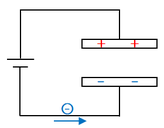
2枚の金属板を電池に接続します。ここに電流を流そうとすると、中学以来の回路の話からすれば、電流は流れません。
金属板の間はすき間が開いていますので、単純に回路が断線状態ですね。
ですが、高校範囲ではもう少し細かいところを見ています。電流は流れません。確かに流れないんですが、完全に流れないわけではなくて、電圧をかけているために、電荷を極板にギュっと押し込む分だけは流れます。
電圧、というくらいですから、圧力をかけているわけですからね。
このように、金属板に電荷を無理やりにでも送っていって、極板に電気が蓄えられることを、充電、といいます。

一度、極板が充電されてしまうと、極板間で向かい合っている正の電荷と負の電荷が、静電気力でお互いに引き合うことになります。
この状態で電池を取り外しても、極板間の電荷は移動することがなく、そのまま極板に蓄えられたままとなります。

その後、電池があったところに抵抗をつなぐと、充電されたコンデンサーは、小さい電池のようなものとしてはたらき、抵抗に電流を流すようになります。
このように、単なる金属板を2枚、向かい合わせておいただけなんですが、それだけで小さい電池のような機能をもつ、この回路素子のことを「コンデンサー」もしくは「キャパシタ―」と呼びます。
コンデンサーの電気量
コンデンサーは、このように、電気をたくわえることができます。
このとき、コンデンサーがどのくらいの電気をたくわえられるか、という量を「電気容量」と呼び、\(C\)と書きます。
この単位を[\(F\)]と書き、ファラドと読むことにしますが、\(1F\)の電気容量というのはとてつもない量で、実際にコンデンサーを扱おうと思ったら、[\(\mu F\)]、もしくは[\(pF\)]を使います。
▼電気容量の単位
[\(F\)]:ファラド
[\(\mu F\)]=\(10^{-6}F\):マイクロファラド
[\(pF\)]=\(10^{-12}F\):ピコファラド
コンデンサーに蓄えられる電気量は、電気容量\(C\)と電位\(V\)の積で表され、\(Q=CV\)と書きます。
ビーカーをイメージすると、ビーカーの容器の大きさが電気容量、ためられた水が電気量、そしてその水の深さが電位、というイメージです。
▼電気量と電気容量
\(Q=CV\)
\(Q\)[C]:電気量 \(C\)[F]:電気容量 \(V\)[V]:電位
コンデンサーの電気容量
この電気容量ですが、極板にどのくらいの電気を蓄えられるかを表す量です。
ということは至ってシンプルな考えですが、極板が広ければ、それに伴って電気容量は多くなります。
コンデンサーは、その極板面積に比例して電気容量が増えます。
また、コンデンサーに電気が蓄えられる原理は、お互いの極板に蓄えられた電気が静電気で引き寄せられていることによるものでした。ということは、極板間の距離が近づくと、静電気力がその分強く働きますので、電気容量は増えます。
コンデンサーは、極板間隔に反比例して電気容量が増えます。
これらをつなぐ係数部分を\(\varepsilon_0\)で表し、これを「真空の誘電率」と呼びます。
これらを立式すると、次のように表せます。
▼コンデンサーの電気容量
\(C=\varepsilon_0\displaystyle\frac{S}{d}\)
\(C\)[\(F\)]:電気容量
\(\varepsilon_0\)[\(F/m\)]:真空の誘電率
\(S\)[\(m^2\)]:極板面積
\(d\)[\(m\)]:極板間隔
▼真空の誘電率
\(\varepsilon_0=8.85×10^{-12}\)[\(F/m\)]
真空の誘電率の数字は、特に覚えておかなくても、問題文に与えられていると思いますので、数字の並びだけうっすらと覚えておけばいいかなと思います。
一応、\(8.85418782×10^{-12}\)「ややこしいやなやつ」という語呂合わせがあります。
が、覚えても役には立たないと思います。
耐電圧
コンデンサーの原理から考えると分かりますが、極板に電荷を蓄えすぎると、やがて限界が訪れます。
電源電圧を\(100V\)、\(200V\)、\(300V\)と、どんどん高くして、無理やり極板を充電していったとします。
すると、やがて極板間で真空放電が起きて、ちょうどコンロやライターのようにカチカチ音を出しながら火花放電し始めます。
そうなると、もはやコンデンサーとしての電荷を蓄える、という機能は失っていることになります。
こうならないための限界の電圧を「耐電圧」と言います。
